今回は、虚数の情緒〜中学生からの全方位独学法〜(吉田武)を読んだ感想を書きます。
1000ページを超える大書です!
概要
表紙はしがき:
『本書は人類文化の全体的把握を目指した科目分類に拘らない「独習書」である。歴史、文化、科学など多くの分野が、虚数を軸に悠然たる筆致で描書かれている。また人生の「参考書」ともなるよう、様々な分野の天才達を縦横に配した。漢字、電卓の積極活用なども他に例の無い独特のものである。時間をかけて読まれることを希望する。』
サブタイトルとはしがきの通り、本書は分野にこだわらず人類文化全体を把握することを目的とした独習向けの参考書です。
とは言えタイトルからわかるように、やはり本書は数学分野の書籍であり、数学を中心としています。現代において世界を記述する上で必須である”虚数”を感覚的に理解すること主軸として、様々な分野を縦横無尽に行き来し全方位の独学を促す教育書です。
本書との出会い
私がこの本と出会ったのは、大学時代の図書館でした。当時数学書のコーナーをよく利用していたのですが、とんでもなく分厚く堂々と棚に鎮座する本書は、図書館を訪れるたびにいやでも目に留まっていました。
ある日ふと本書を開いてみると、いきなり巻頭言の書き出しに衝撃を受けました。
『さあ諸君、勉強を始めよう勉強を。』
この一行に完全に胸を打たれ、時間有り余る大学生時代の私は1000ページにも及ぶこの大書を読み進めました。本書の感想を一言でいうと、『内容が充実している!』です。決してただの分厚い本ではないです。数学のみならず多分野の興味深いトピックスが並んでおり、視野が大きく広がったように感じました。
最近になって、また読み返したくなり古本屋で一冊手に入れて再度読みました。
ただ、やはり1000ページを超える大書ともなると、すぐに読めるようなものではなく、毎日少しづつ読み進めて、結局読了に1ヶ月を要してしまいました。。。ただ読み終えた達成感は大きく、2回目ではありましたが幾つか新たな発見もあり、心が満たされたように思いました。
本書は三部構成となっていて、それぞれが単体でとても充実しているので、それぞれについて内容と感想を記載しようと思います。
第Ⅰ部(独りで考えるために)p21~p124
この第Ⅰ部は方法序説として位置づけられており、筆者が初学者に向けて伝えたいことが詰め込められた章になります。一言でいうと”地道に勉強して視野を将来に向けて拡げろ!”みたいなことが書かれています。第Ⅰ部は若干過激めでもあり説教くさい感じもありますが、内容には概ね同意できました。
筆者の言葉:
『若し学問に王道あらば、それは未舗装の泥道に違いない。』
が最も心に響いたフレーズでした。
筆者は特にコミュニケーションツールとしての日本語を重んじており、本書では先人達のメッセージを受け取るために言葉がいかに大切かということを説いています。近年の言葉の乱れを一方的に批判するような、いわゆる『最近のお若者は・・・』的な記述もあり、若干の嫌悪感を感じる部分もありました。これまで日本語が様々に形を変えて現代まで伝わってきた文化とも言える言葉の変遷を考えると、ちょっと視野が狭いのではと疑問に思う点もありますが、一方で先人達のメッセージを受け取るためには言葉を理解する必要があり、さらには次世代にメッセージを伝えるためには現在の日本語を守っていく必要はあるように思います。今、平安時代の古典文学を原文読もうと思っても簡単には読めませんし、百年前の夏目漱石を読もうと思っても、村上春樹を読む5倍くらいの時間がかかってしまいます。(最近『我輩は猫である』を読んでいますが、1日かかって100ページ程度しか読めませんでした。)個人的には文化や環境に応じて変化してきた日本語の変遷を鑑賞すること自体が楽しく感じたりしますが、やはりいたずらに言葉を乱すことには問題はあるように感じます。
(ところで、日本以外の言葉は昔と今でどのように変化してきているのだろうと興味が湧いたりもしました。英語の基はラテン語??)
もう一つ印象的だったのは、筆者が文系・理系の二分化を極端に嫌っているということでした。
『他人を文系だ、理系だと二分して何が愉しいのだろう。』
などと皮肉を含めて批判しています。
日本では進路を決める前準備として高校でこの二分化が行われますが、個人的にはこの仕組み自体に反対では無いし、むしろ効率的で良いと思っています。結局その先では大学の何学部に入るか、職業として何を身につけるかという選択があるわけで、何を中心として学ぶかという二分化はむしろ将来誰もが直面する細かい選択へ向けた助走として重要だと感じます。ただ、『自分は文系人間でして。。。』などと先天的に二分化されていたかのように言い訳に使うのは違うかなと思っています。(もちろん反対も同じ。)ただ高校の時に、何を中心に学ぶかの選択をしただけの話で、将来の視野を狭めるためのラベル付けではないという意味では筆者に同意できました。
第Ⅱ部(叩け電卓!掴め数学!)p125~616
p125にしてようやく本題に入ります笑。ここまではあくまで序章にすぎません。
複素数に関する勘違い
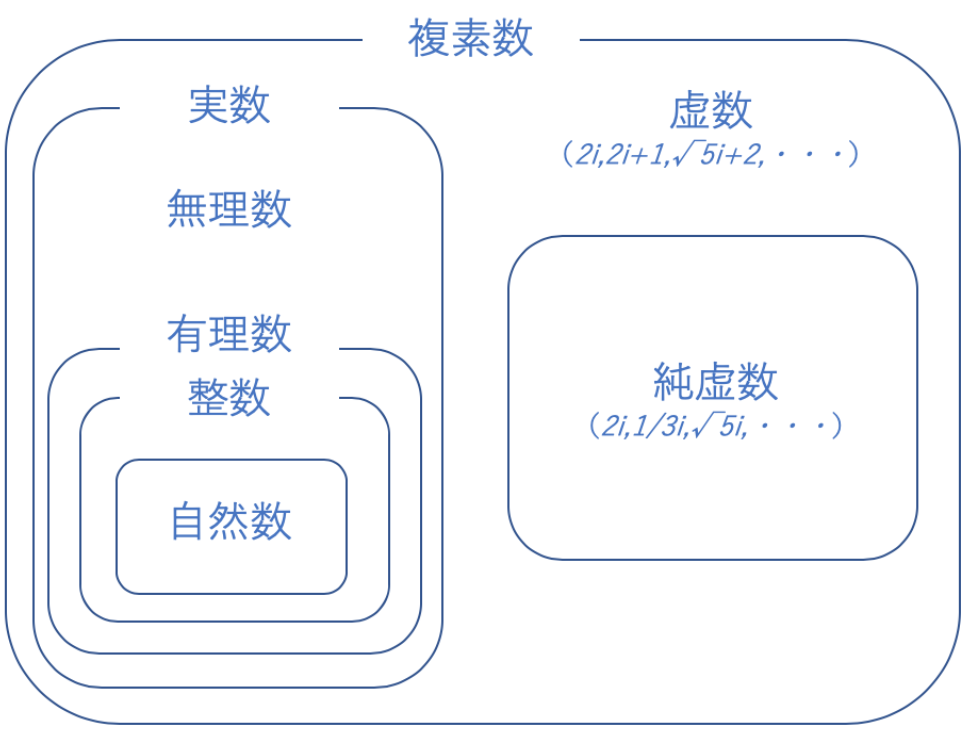
濃度の概念との出会い
$$\aleph$$
カントールの対角線論法(背理法による証明)

実数全体の濃度
第Ⅲ部(振子の科学)p617~p965
第Ⅱ部で虚数とは何かが理解できたところで、ようやくこれを物理学という形で現実の世界に応用し、”虚数の情緒”を感じることになります。
この第Ⅲ部で取り扱うのは振子を中心とした物理となりますが、虚数がこの現実の世界に”確かに存在”しているということを実感することができました。ここで最も重要となるのが、
$$e^{±iθ}=cosθ±isinθ$$
この、オイラーの公式です。
振り子の動きを記述し、さらには量子力学のシュレーディンガー方程式の解ともなることが、物理学の発展歴史と共に丹念に説明されています。第Ⅱ部同様に面白いトピックスが多すぎて、この記事に何を書くか大変迷うところではありますが、最も印象に残った”フーコーの振り子”について少し紹介します。
フーコーの振り子
これは振り子を使って地動説を証明した実験で、地球19世紀の物理学者フーコーによって行われました。
”地動説”は17世紀ガリレオによって天文学的な知見から唱えられ始めたことで有名ですが、このフーコーの振り子は天文学ではなく、全く単純な振り子の物理実験から地動説を証明した実験です。
まず、わかりやすい例として、北極に振り子を設置し、ある日の午前零時に振動を開始させたとします。
【午前零時】
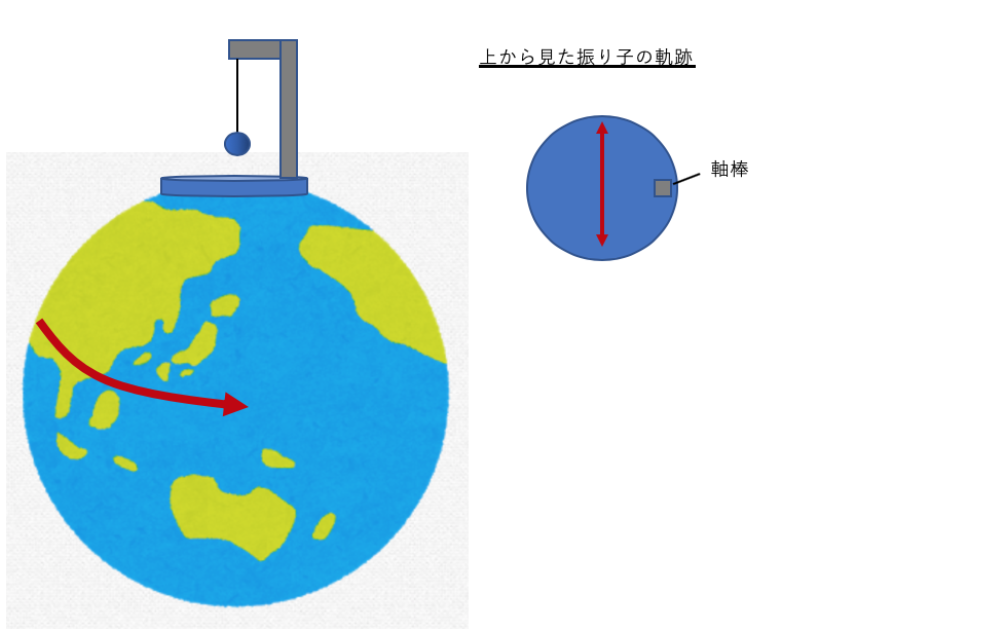
その後振り子を振動させた状態で午前6時まで待つと、地上で観測している実験者にとっては異変が起きます。下図のように振り子を上から見た軌跡が90度回転するという現象が起こるのです(軸棒の位置に着目!)。宇宙から見れば軌跡に変化ありませんが、地上で観測していると軌跡が回転するように見えます。
【午前6時(地球が1/4回転)】
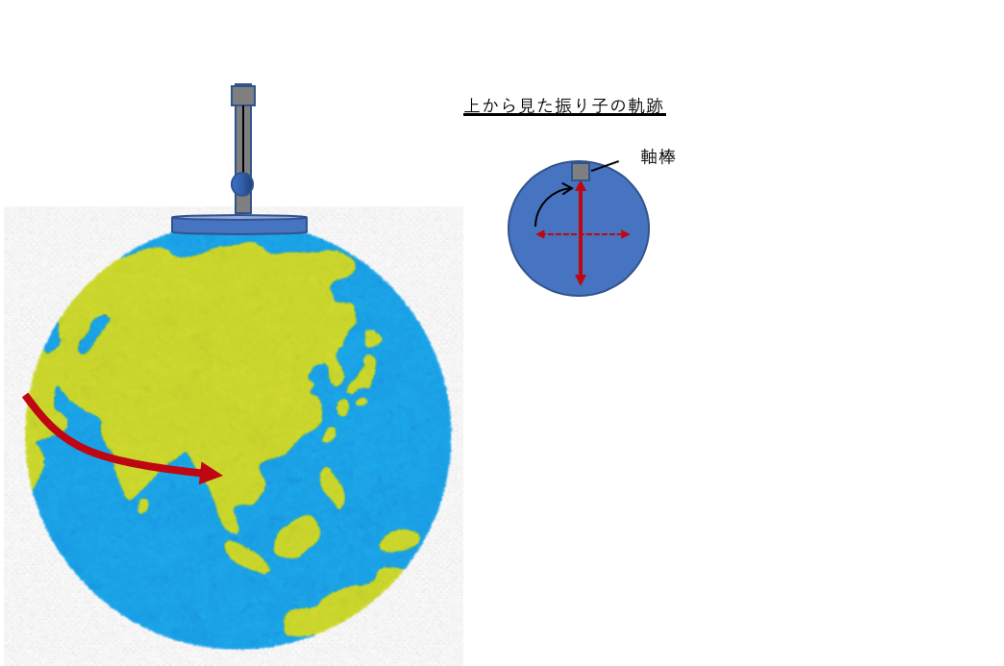
ということでこれは地球が自転しているということを直接的に示していると言うことが出来、地動説の証明となります。
この実験をフーコーは長さ67m、重さ28kgの振り子を使って行ったとされています。
単純ではありますが中々壮大な実験ですよね笑。フーコーには成功する確信があったのでしょう。
ちなみに振り子の軌跡の回転周期は”緯度”によって変わり、当然ながら赤道で実験をすると軌跡は回転しません。東京ならば一回転の周期は40時間程度になります。*1ぜひお試しあれ。(壮大な準備が必要になりますが笑)
他にも振り子の物理を応用し著者が独自に研究を進めた、野球のバッティングに関する考察なども大変興味深い内容でした。
ただ全体を通して見ると第Ⅲ部の内容は、第II部とは異なり本書のみでは物足らないと感じる部分が多くあったように思います。電磁気や相対論、量子論に関してなど、多分野の解説が豊富にあり、なるべく簡単に内容を説明してくれてはいますが、本当に理解するためには別の書籍や、専門書を当たる必要があると思います。一方で物理学への入門としては最適であると感じました。広く浅くそして面白い内容となっており、もっと勉強したいという気持ちにさせてくれました。私自身としては電磁気学の理解が浅く専門書で一から勉強してみようかなと考えています。
まとめ
総じていうと、本書は1000ページを超える大書でありながら内容は充実していて密度が濃く、世界の見え方が変わるほどのインパクトを持ち合わせている教育書であると感じました。
全1001ページ(5cm)
東海大学出版(2000/3/1)
おすすめ度:★★★★★
内容の充実度:★★★★★
読了後の達成感:★★★★★