夕方にふと空に目をやると夕焼けがとても美しく見える時ってありますよね。そんなとき私はついつい写真を撮ってしまう習性があって、スマホの写真フォルダの中には特に何に使うでもない夕焼け空の写真が沢山たまってしまっています。
そんな写真を見ていて私はふと思いついたことがあります。
日の入りを観察すれば太陽の大きさを求めることができるのではないか?
この人は何を言っているのだろう?って感じですよね笑。
これだけでは何を言っているのか全くわからないと思いますが、この突然のひらめきを順を追って説明します!

思いついた方法
今回思いついた方法というのは、太陽が地平線に沈む時間を測定することで、それを太陽の直径に換算してサイズを導くことができるのではないか?という方法です。
順を追ってその方法を説明しよう!
まず夕日が地平線に沈み始めて沈み終わるまでの、ちょうど下図に示すstartからfinishの状態までの時間をストップウォッチで測定します。(おそらく数十秒〜数分)
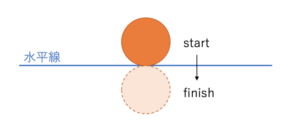
この時間を\(t\)分とすると、地球から見ると太陽はぐるりと360°を24時間かけて回っているように見えますので、下図に示す観測角\(θ\)は、
$$θ=360°×t÷(60×24)$$
となります。
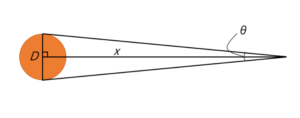
太陽の直径:D 太陽までの距離:x 観測角:θ
太陽の直径を\(D\)とすると、正弦定理から
$$\frac{\frac{D}{2}}{sin(\frac{θ}{2})}=\frac{x}{sin(90°-\frac{θ}{2})}$$
の関係が成り立ち、整理すると、
$$D=2x×tan(\frac{θ}{2})・・・★式$$
と表すことができます。
ここで地球から太陽までの距離xが必要になってくるわけですが、太陽光が我々の目に届くまでにかかる時間は8分であること*1を思い出すと簡単に導くことが出来て、
$$x = 8min × 60sec/min × 30万km/sec(光速)=14400万km$$
と計算することができます。
つまりあとは、日の入りの時間\(t\)を計って観測角\(θ\)を得ることができれば★式から、太陽の大きさである直径\(D\)を求めることが出来るはずなのです。ということで実際にやってみました!
ここで注意!
今回の計算モデルはあくまでも近似です。
実際には黄道は若干傾いていますので、太陽は水平線に対して垂直に沈むわけではありませんが、今回はそこは無視をして太陽が天の赤道を通っていると近似をした簡略なモデルで計算を進めました。
黄道の傾きも考慮して計算することも可能だと思いますが、計算が面倒になりそうなので今回は止めました(すいません)。
使用するもの
・ストップウォッチのみ
・サングラス(太陽を直接見ると目に悪いので)
測定場所
冒頭に旅行で行った江ノ島での夕日写真を載せましたが、これはiphoneに眠る数多くの思い出の夕日写真の一つですので今回の測定とは関係ありません笑
今回は家の近くで夕日を観測して太陽のサイズを測ってみることにしました。
結果
日の入りの時間を目視で計って見ましたところ、\(t=2.0min\)程度であることがわかりました。すると\(θ\)は、
$$θ = 360°×2÷(60×24) = 0.5°$$
となります。これを使って太陽の直径\(D\)を求めると、
$$D = 2 × 11400万km × tan(\frac{0.5}{2})= 99万km $$
という結果が導かれました!
地球の直径はだいたい1万kmくらいなので、これが本当なら太陽は地球の100倍くらいの大きさということになりますが、果たして。。。
答え合わせ
さて、思いつきで導いた答えは答えは合っているのでしょうか。googleで検索して太陽の直径を調べてみると、、、
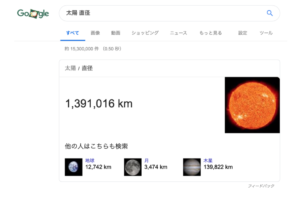
結果は139万km。私が算出したものよりは少し大きな結果ですが、誤差-30%程度とまずまずの結果ではないでしょうか??一回しか日の入りを観測していないので何回か観測して精度を高めてやればもう少し真の値に近づいたかもしれません。がある程度満足できる結果だと感じました。
まとめ
太陽の大きさを日の入りの時間を使って測ってみた結果、そこそこの精度で答えを求められることがわかりました。自由研究とかで困ったらさも自分で思いついたかの様に是非使ってみてください笑。頑張れば月でもできるかもしれないですよ!
この方法って実践した人いるのかな?というか一般的に知られている方法なのかな?と思ってざっとネットを調べる限りは出てきませんでした。ということで勝手に名前をつけちゃうことにします!(たぶんだれかやってると思うけど)
命名:『日の入り正弦法』ということでいかがでしょう。
こういった天体ネタが私はとても好きなので、また何か面白いことを思い付けば記事にしようと思います!