カワダ製サイコロを１万回振って目の出やすさを調べてみた（苦行）！

読者の皆さんの中にも同じような疑問を感じている方が少なからずおられるのではないでしょうか。

サイコロと言えば、幼い頃から慣れ親しんできたボードゲームのお供ですが、私はかれこれ長い間、この疑問を頭の片隅に持ち続けていました。不均一に穴ぼこが彫られた四面体なのですから目の出やすさにバラツキがあってもなんら不思議ではありません。

皆さんも気になりますよねぇ？
いいでしょういいでしょうわかりました、私が実際に調べてあげましょう！

仮説

サイコロの面には数字の分だけ穴がくり抜かれていて、そのため数字の小さい面ほど重量が重くなっていて下を向きやすいと考えることができます。また、サイコロの対面の和は常に7となるように数字が配置されていることを考えると、サイコロの目の出やすさは

$$6>5>4>3>2>1$$

となることが予想されます。

要するにこれは、
穴が少なくて重い小さい目の面ほど下を向き易いのではないか？という仮説です。

という事でこの仮説を確かめるために、今回想定しているサイコロに合致する数が大きいほど面の重量が軽くなっているであろうサイコロを近くのお店で複数個購入してきました（カワダ製 ¥95/6個）

実験方法

準備するもの

・サイコロ×5

・お椀

・PC（集計用）

・一万回チャレンジに立ち向かう勇気！

手順

①サイコロを5個選び、No.1~No.5の印をつける。

②各サイコロを2000回づつお椀へ投げて、出た目を記録する。

③合計1万回分の結果を集計し考察する。

※一つのサイコロで実験するとサイコロ固有の歪みが色濃く反映されて仮説を検証できない可能性があると思ったので、念のため5個に分散させて検証しました。

結果

まずは、No.1~No.5それぞれの結果を1000回ごとに区切ってまとめた結果です。
それぞれのサイコロを2000回づつ振っているので、サイコロ５個×二枚のグラフで合計１０枚のグラフを下に示します。

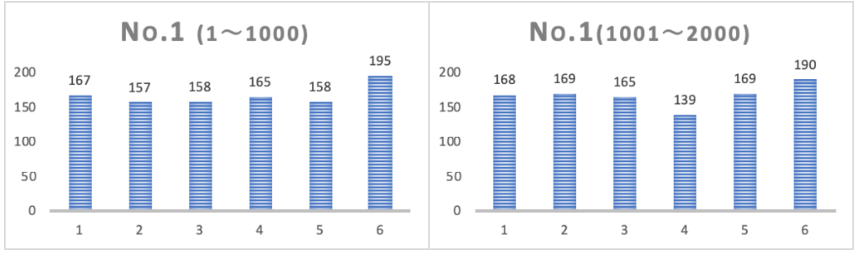
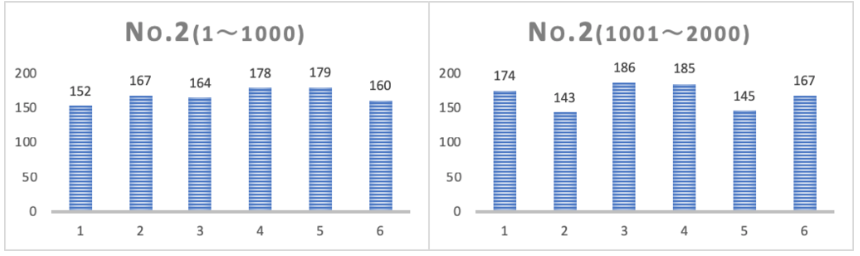
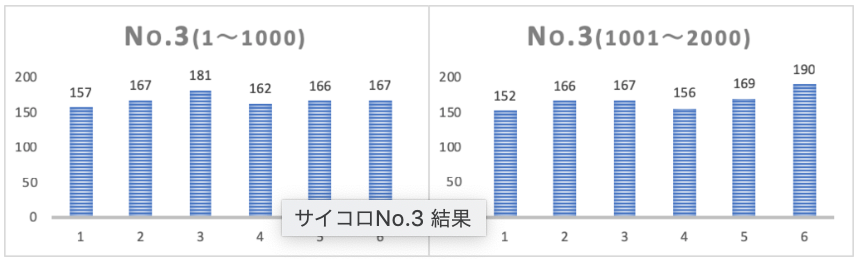
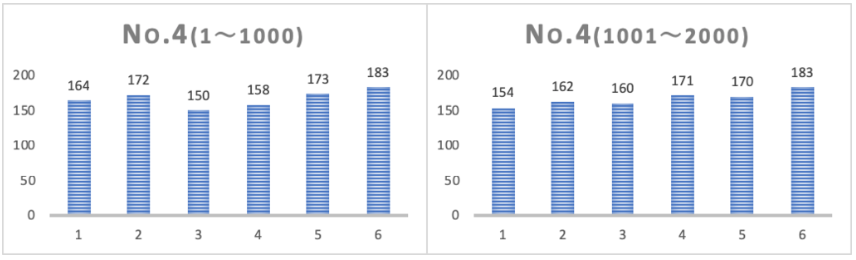
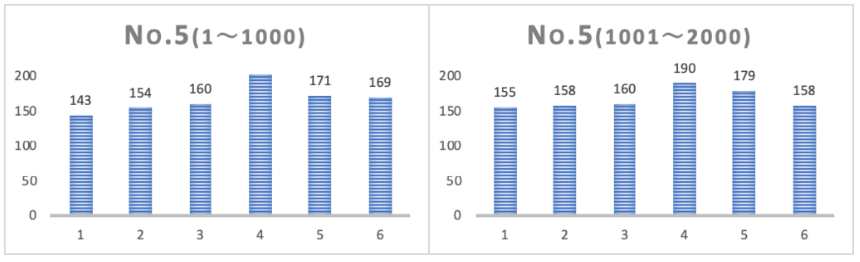
結果ご覧になって如何でしょう？なかなかはっきりとした傾向は出ていない様で考察が少し難しそうです。

でもじっくり結果を眺めてみると、
サイコロのNoによって目の出やすさの傾向は若干違っているようです。
同じサイコロで1000回ごとに集計したグラフを左右で見比べてみると、ある程度形が似通っていて、それぞれのサイコロに特有の傾向があるみたいです。おそらくサイコロの微妙な歪みや角の曲率などが影響しているのではないかと思います。

では、上の結果を重ね合わせてやって、サイコロ１万回振った結果をまとめます！

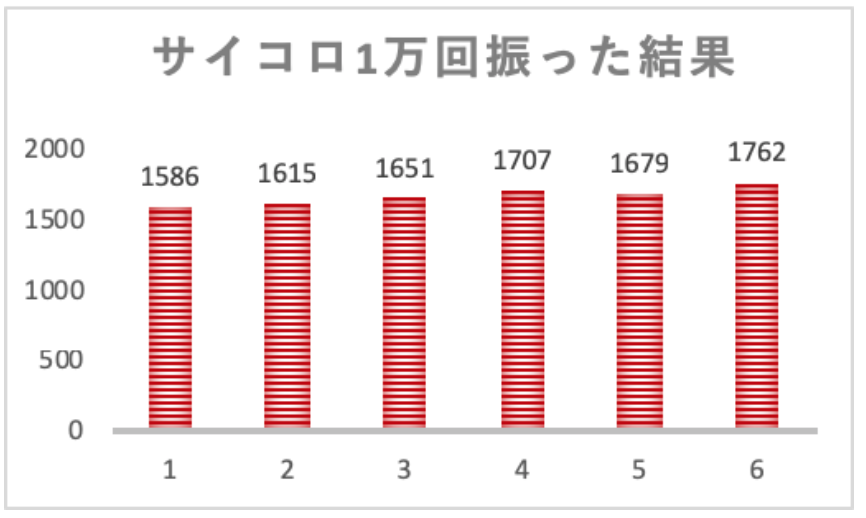
ということで、全体の結果を集計したものが上の図になります。

若干ではありますがやはり数が大きい目ほど出やすい傾向がありそうです。

とは言えバラツキは思ったより小さく、だいたい均一で気にするほどのものではないかなという印象です。

まとめと感想

やはり仮説の通り、数が大きい目の方が出やすいことがわかりました。しかしながらそれぞれのNo別の結果からわかるように、サイコロ一つ一つの固有の歪みの方がむしろ目の出やすさには大きく影響を及ぼしているようです。従って一つのサイコロで試行する場合には、面の重さによる目の出やすさは隠れてしまう程度のように思います。まあ大雑把に言えば、目の出やすさはだいたい均一で、あまり気にするほどのことではないという印象でした。

ゲームなどで使用する場合には、特に考慮する意味もないくらいの影響かなと思います。でもこの実験を行なった本人としては、6が最も出やすいということを信じて、今後サイコロを使用させていただこうと思います（ｷﾘｯ）

最後に

サイコロを投げてはテンキーで入力、投げては入力と延々繰り返す作業になりますが、目がしょぼしょぼしてくるわ、腕に疲れがたまってくるわでとても辛いです。1000回サイコロを振るのに大体30分ぐらいかかるのですが、１万回となると5時間ぐらいかかります。とは言えとてもとても連続で振り続けることはできないので、この実験３日がかりで行う羽目になってしまいました。

実験をやった感触からいうと、今回の十倍の１０万回くらい試行すれば、さらにしっかりした結果が出てくるのではないかと思います。単純に考えると今回の実験の十倍の50時間、丸二日以上の時間が必要になる実験ということになりますが。。。

やりたい方はご参考までに。私は絶対にやりません笑

あと考察としては、今回の結果とエクセルなどのランダム関数などで生成した試行と比較してみて明瞭な差が出てくるかどうかと言った着眼点で見てみるというのも面白いかも知れません。

ただもう力尽きてしまったので、さらに突っ込んだ考察は気が向けば追記させていただきます。期待せずお待ちください。