素数演算をVBAで24時間実施したら、どれだけ大きい素数に辿り着く？

それは未だ人類がその規則性を見出すことの出来ていない神秘の数。
素数とは、1と自分自身以外に正の約数をもたない自然数(1は除く)のことで、すなわち「2」,「3」,「5」,「7」・・・のことを指します。

みなさんもおそらく小学校か中学校ぐらいでこの定義について習ったことをなんとなく覚えているのではないかと思います。でもこの素数を導く公式については習ったことがないのではないでしょうか？
でもそれは当たり前、なぜならそんな公式は未だかつて見つかっていないからなのです。ということは、どの数が素数でどの数が素数でないかについては、上に示した定義に従ってひとつひとつ確認していくしか方法がありません。それに加えてなんと素数は無限個あります！どこまでいっても終わりがありません。

だがしかし！幸運にも現代にはPCという計算環境が整った機器が身近にあります。

ということで今回は、
自分のPCを使ってどこまで素数を演算できるかチャレンジしてみました！

目標

筆者調べによると、2019年現在これまでに見つかっている最大の素数は、素数が出現しやすい式としてよく知られるメルセンヌ数（\(2^n-1\)）の\(n=82,589,993\)の値のようで、10進数の桁数でいうと二千万桁というとんでもない数です。（2018/12,GIMPSによる^[1]https://www.mersenne.org/primes/?press=M82589933）

こんな数に到達することは我々の普段使っている汎用PCでは不可能ですが、かつて18世紀の大数学者オイラーは手計算でn=31のメルセンヌ数が素数であることを発見しています。この数は、
$$2^{31}-1 = 2,147,483,647$$
となり、10桁の数字になります。

オイラーが手計算で発見したこの数を目標に、2,3,5,7,11・・・と自分のPCで一つづつ順番に24時間計算させてみることにします。

方法

今回はエクセルを使って計算をしてみることにしました。Mac-PCでエクセルVBAを使用するというかなりの特殊条件でトライしてみることとします。笑

計算プログラムは非常に簡単なアルゴリズムで実施しました。内容を簡単に説明すると、注目する自然数pを、2~√pの間の自然数mで割ってやって、割り切れるかどうかをしらみつぶしに確認しています。この確認をp=2,3,4,5,6,7,8,9・・・と延々と繰り返し、pが素数か素数でないかを判定して、素数ならばエクセルのセルに記入をするというプログラムを書いて実行しました。ソースコードは下図の通りです。

計算環境

VBAコード

Sub 素数() 
Dim r As Long, c As Long, m As Long, p As Long 
Dim flag As Boolean 
r = 1 
c = 1 
p = 2 
Do 
　flag = False 
　For m = 2 To Int(Sqr(p)) 
　　If p Mod m = 0 Then 
　　　flg = True 
　　　Exit For 
　　End If 
　Next 
　If flag = False Then 
　　Cells(r, c + 1) = p 
　　Cells(r, c) = Now 
　　r = r + 1 
　　If i > Rows.Count Then 
　　　r = 1 
　　　c = c + 2 
　　End If 
　End If p = p + 1 
Loop Until p > 10 
End Sub 

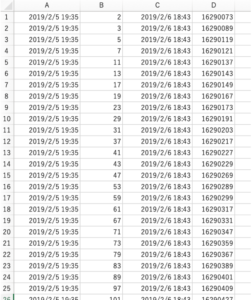
計算の様子

結果&勝敗

求めた素数：1,473,238個

得られた最大の素数：23,424,259

24時間も計算をさせただけあって、かなり沢山の素数を見つけることができました！

だがしかし！オイラーが求めたn=31のメルセンヌ数2,147,483,647には二桁も届かない結果です。PCを使ったにも関わらず手計算に負けてしまいました、、、恐るべしオイラー。

やはり一つ一つしらみつぶしに確認していく様な何の工夫もない方法では、PCとは言え天才の脳みそには敵わないようです。

経過監視

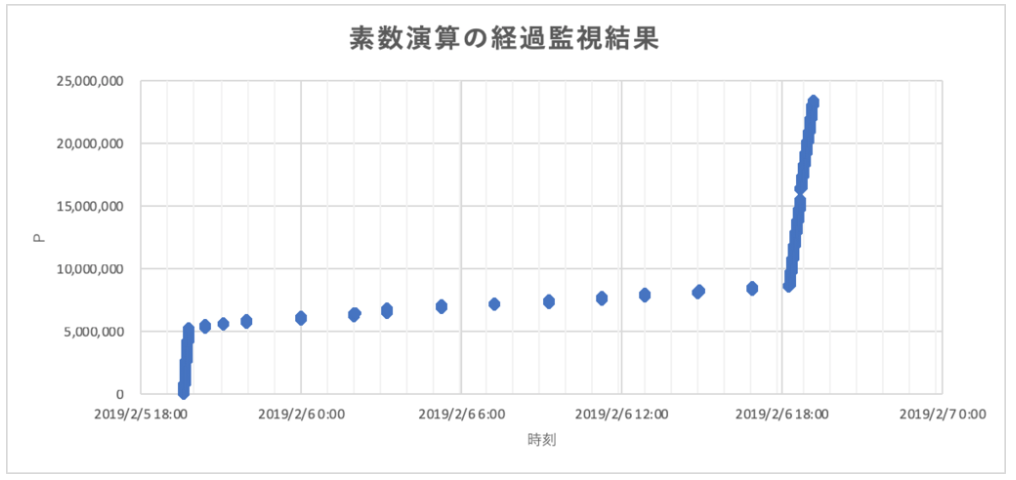
今回は、経過監視が出来るように素数が見つかったらその時刻を打刻するようなプログラムを書いたので、素数発見の時間的な流れが確認できます。

その結果を確認すると衝撃の事実が！！PCの”サボり”が発覚しました。
結果のグラフを見てみると、2019/2/5 19:00頃に計算を開始して一時間ぐらい順調に計算が進んでいますが、その後大幅に失速。翌日18:00頃、スピードを取り戻してラストスパートという流れになっていました。これは私が会社に行っている間だけ明らかに計算をサボっています。まったく何をやっているんだ、私のPC君！

真面目なことを言うと、たぶんPCがスリープ状態か何かに入って処理速度が遅くなってしまっているのだと思います。

もうちょっと頑張って欲しかったな笑

 まとめ

手計算のオイラーに敗北するという残念な結果になってしまいました。オイラーがすごいというのも勿論ありますが、今回はPCが20時間以上計算をサボっていることが発覚しましたので、是非再トライしてみたいなと思っています。

あと、今回のチャレンジをする中でMac版でのエクセルVBAはちょっと扱いづらいなという印象がありました。仕事上Windows-Office系のソフトを使い慣れているというのもあって今回はエクセルを使ってみましたが、Macでは互換性がいまいちの様です。グラフが動かなかったり、プログラム中断のショートカットが無かったりと、別の意味で苦戦しました。。。今度やるならWindows-PCでやりたいなと思います。もしかすると途中計算速度が遅くなったトラブルもWindowsでは解消されるかもしれません。近々挑戦したいです！